La geometría, una de las ramas fundamentales de las matemáticas, se encarga del estudio de las formas, los tamaños, las posiciones relativas de los objetos geométricos y las propiedades del espacio. Dentro de esta disciplina, uno de los conceptos clave es la bisectriz.
En términos simples, una bisectriz es una línea, rayo o segmento que divide algo en dos partes iguales o proporcionales.
El término "bisectriz" proviene del latín "bisectus", que significa "cortar en dos". La bisectriz se emplea en distintos contextos geométricos para dividir ángulos, segmentos, arcos y otros elementos en partes iguales o proporcionales.
A continuación, exploraremos cómo se aplica la bisectriz en diversas situaciones geométricas.
Bisectriz de un ángulo
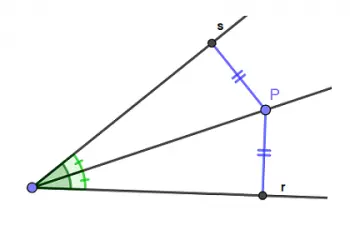
Una de las aplicaciones más comunes de la bisectriz en geometría es la división de ángulos. La bisectriz de un ángulo es una línea que divide ese ángulo en dos ángulos más pequeños que tienen la misma medida.
En otras palabras, divide el ángulo en dos partes iguales. Esto es útil para la trisección de ángulos, la construcción de ángulos específicos y la resolución de problemas geométricos.
La bisectriz de un ángulo se puede visualizar como una línea que parte desde el vértice del ángulo y divide este en dos ángulos congruentes.
Bisectriz de un segmento
La bisectriz también se puede aplicar a segmentos de línea. La bisectriz de un segmento divide dicho segmento en dos partes de igual longitud. Si tenemos un segmento AB, la bisectriz lo dividirá en dos segmentos AC y CB, donde AC es igual en longitud a CB.
Esta propiedad es especialmente útil para encontrar el punto medio de un segmento, lo que tiene implicaciones significativas en la geometría analítica y la construcción de figuras geométricas equidistantes.
Bisectriz de un arco
En geometría circular, una bisectriz de un arco es una línea que corta el arco exactamente a la mitad. Esto es de gran utilidad en problemas de geometría donde se requiere una división precisa de un círculo o arco.
La bisectriz de un arco se utiliza, por ejemplo, para determinar el centro de un círculo o para dividir un círculo en dos arcos de igual longitud. Esto es fundamental en la construcción de figuras geométricas circulares y en la resolución de problemas relacionados con círculos.
Bisectriz en triángulos
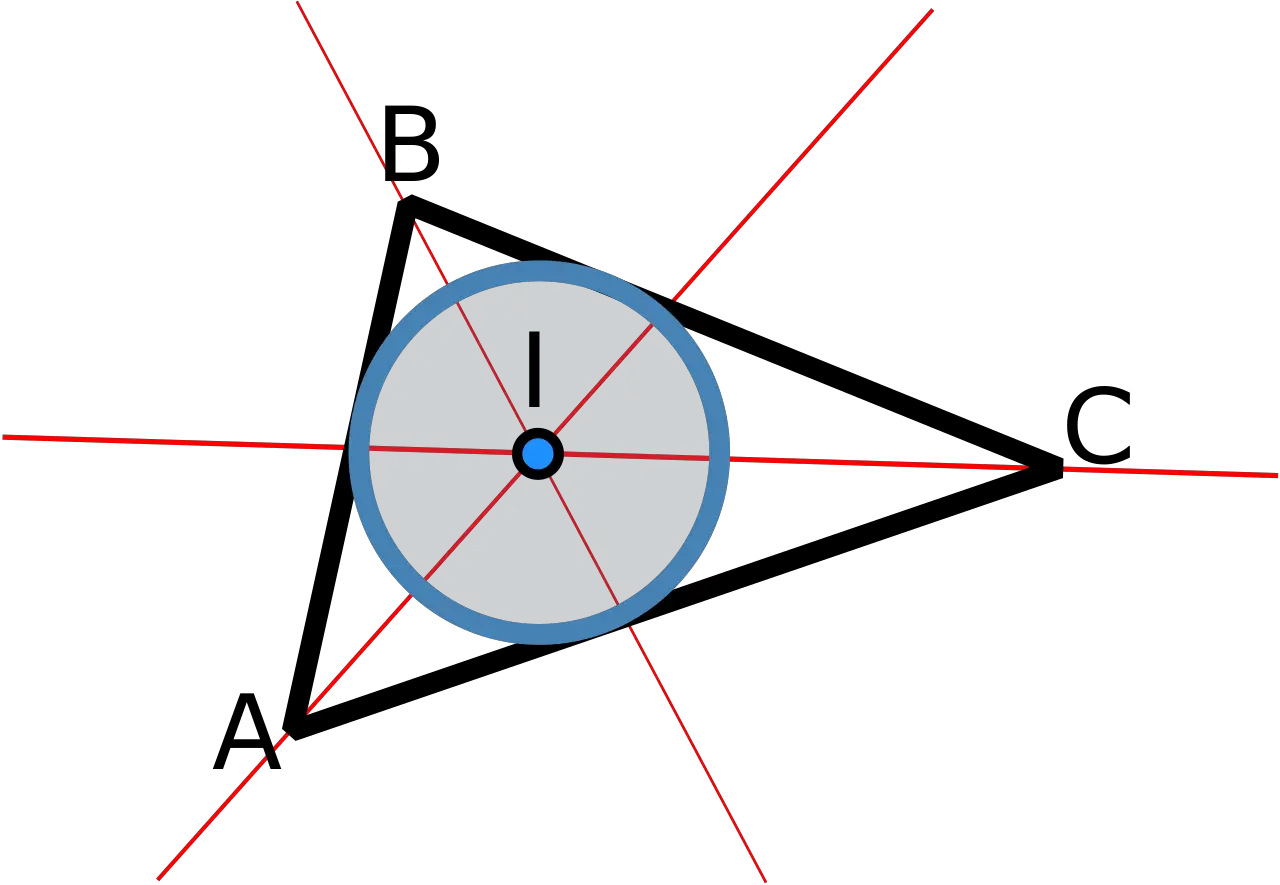Este elemento también juega un papel importante en el estudio de los triángulos.
En un triángulo, la bisectriz de un ángulo es una línea que parte desde el vértice del ángulo y divide el lado opuesto en dos segmentos que son proporcionales a los otros dos lados del triángulo. Esto se conoce como el "teorema de la bisectriz" y es útil para resolver problemas de trigonometría y demostrar propiedades de los triángulos.
El teorema establece que la razón entre la longitud de un lado del triángulo y la longitud del segmento que la bisectriz forma en ese lado es igual a la razón entre los otros dos lados del triángulo.
Esta propiedad es de gran importancia en la resolución de problemas geométricos que involucran triángulos y sus características.
Aplicaciones de la bisectriz en la vida cotidiana
Por ejemplo, en arquitectura, se utiliza para construir ángulos precisos y divisiones proporcionales en planos y diseños de edificios. La bisectriz permite a los arquitectos y diseñadores crear estructuras simétricas y equilibradas con facilidad.
En la ingeniería, la bisectriz se utiliza para determinar puntos equidistantes en estructuras y máquinas, lo que es esencial para garantizar la estabilidad y la precisión en diversas aplicaciones.
Conclusión
La bisectriz es un concepto fundamental en geometría que se utiliza para dividir ángulos, segmentos, arcos y otros elementos en partes iguales o proporcionales.
Su aplicación es amplia y versátil, desempeñando un papel esencial en la resolución de problemas geométricos, la construcción de figuras geométricas y la demostración de propiedades matemáticas. Comprender la bisectriz es fundamental para aquellos que deseen adentrarse en el mundo de la geometría y su aplicación en diversas disciplinas.
Desde la división precisa de ángulos en arquitectura hasta la resolución de problemas de trigonometría en matemáticas, la bisectriz es una herramienta poderosa que desempeña un papel destacado en la resolución de problemas y la creación de estructuras equilibradas y simétricas.
