En el campo de la geometría, los planos son unos elementos básicos y fundamentales. Definidos como superficies infinitas y planas que se extienden en todas las direcciones, los planos son elementos fundamentales que nos ayudan a comprender las formas y estructuras en dos dimensiones.
En este artículo, explicaremos qué son los planos en geometría, sus características distintivas y cómo se aplican en diversos contextos matemáticos y prácticos. Desde el diseño de figuras geométricas hasta la resolución de problemas y el desarrollo de aplicaciones tecnológicas, los planos desempeñan un papel vital en nuestro entendimiento del espacio y la forma.
¿Qué es un plano?
En geometría, un plano es una superficie plana e infinita que se extiende en todas direcciones.
Puedes pensar en una hoja de papel que se extiende para siempre, sin tener grosor. En este caso, no hay límites ni bordes, ¡es como un mundo infinito en dos dimensiones!
Características de un plano
Las principales características que definen un plano en el espacio son las siguientes:
- Infinito en todas direcciones: Una de las características más importantes es que se extiende infinitamente en todas direcciones. Esto significa que no importa cuánto te alejes de un punto en el plano, siempre encontrarás más espacio.
- Sin grosor: A diferencia de los objetos tridimensionales, como una pelota o un cubo, un plano no tiene grosor. Imagina que estás mirando un dibujo en una hoja de papel. El dibujo está en el plano del papel, pero el papel es tan delgado que podemos considerar que no tiene grosor.
- Representado por líneas: En la geometría, representamos los planos usando líneas. Estas líneas pueden ser rectas o curvas y se extienden en todas las direcciones dentro del plano. Cuando dibujamos figuras geométricas en un plano, usamos estas líneas para mostrar cómo se relacionan entre sí.
- Independiente del sistema de coordenadas: Un plano es independiente del sistema de coordenadas utilizado para representarlo. Esto significa que, independientemente de cómo se elijan los ejes x e y, las propiedades básicas del plano, como su infinitud y su falta de grosor, permanecen inalteradas.
- Contiene infinitos puntos: Dado que se extiende infinitamente, contiene infinitos puntos. Cada punto en el plano es único y puede ser identificado por sus coordenadas, si se utiliza un sistema de coordenadas.
- No determina una dirección preferencial: A diferencia de las líneas y segmentos, que tienen una dirección específica, el plano en sí mismo no tiene una dirección preferencial. Puede considerarse como una superficie sin orientación en la que las direcciones son igualmente válidas.
Tipos de planos
En geometría, existen varios tipos de planos que se utilizan para diferentes propósitos y aplicaciones. A continuación, se describen algunos de los tipos más comunes:
- Horizontal: Un plano horizontal es aquel que se extiende horizontalmente en relación con la superficie terrestre. En un sistema de coordenadas tridimensional, un plano horizontal no se inclina ni se desvía verticalmente.
- Vertical: Contrario al anterior, un plano vertical se extiende verticalmente y es perpendicular a la superficie terrestre. El vertical es útil en geometría para representar relaciones espaciales en el espacio tridimensional.
- Inclinado: Un plano inclinado es aquel que no es ni horizontal ni vertical, sino que forma un ángulo con respecto a ambos. Los inclinados son comunes en problemas de física y mecánica, donde se utilizan para estudiar fuerzas, pendientes y movimiento.
- Cartesiano: este tipo es un sistema de coordenadas bidimensionales que consiste en dos ejes perpendiculares, generalmente etiquetados como x e y. Se utiliza ampliamente en matemáticas para representar puntos, gráficos y funciones.
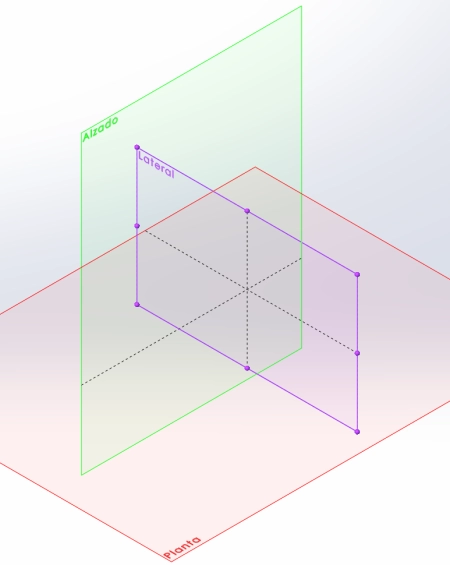
- Proyección: En dibujo técnico y diseño, un plano de proyección se utiliza para representar objetos tridimensionales en dos dimensiones. Los planos de proyección incluyen tres planos: planta, alzado y lateral, que muestran diferentes vistas del objeto desde distintos ángulos.
- Tangente: Un plano tangente es aquel que toca una superficie en un solo punto y es perpendicular a la línea que pasa por ese punto. Los planos tangentes son importantes en cálculo y geometría diferencial para representar la relación entre curvas y superficies en un punto dado.
- Paralelo: Un plano paralelo es aquel que no se cruza con otro plano dado y mantiene la misma distancia en toda su extensión. Los planos paralelos son útiles en geometría para estudiar propiedades de líneas y ángulos en relación con superficies paralelas.
- Perpendicular: Un plano perpendicular es un tipo especial que forma un ángulo recto (de 90 grados) con respecto a otro plano o a una línea.
Diferencia entre plano y área
En geometría, el término "plano" se refiere a una superficie bidimensional que se extiende infinitamente en todas direcciones, como una hoja de papel. Es una entidad abstracta sin grosor, definida por la intersección de dos líneas o por sucesiones de puntos en el espacio.
Por otro lado, el "área" es una medida cuantitativa de la extensión de una superficie bidimensional. Representa la cantidad de espacio cubierto por una figura en el plano y se expresa en unidades cuadradas (como metros cuadrados o centímetros cuadrados).
Mientras que un plano es la superficie en sí misma, el área es la medida numérica de cuánto espacio ocupa esa superficie.