La geometría es una rama de las matemáticas que se enfoca en el estudio de las formas, tamaños y propiedades de los objetos geométricos, como puntos, líneas, segmentos, polígonos y círculos.
Uno de los temas fundamentales en geometría, i en particular de los triángulos, es el estudio de los ángulos y segmentos, y uno de los teoremas más importantes relacionados con estos conceptos es el teorema de la bisectriz.
Este teorema desempeña un papel crucial en la división de ángulos y segmentos, y tiene aplicaciones en diversas áreas de las matemáticas y la física.
Definición de ángulos y bisectriz
Antes de sumergirnos en el teorema de la bisectriz, es importante comprender algunos conceptos clave en geometría. Un ángulo es la región formada por dos rayos que comparten un punto en común, llamado vértice. Los ángulos se miden en grados, y un ángulo completo es de 360 grados. En muchos casos, necesitamos dividir un ángulo en dos partes iguales, y eso nos lleva a la noción de una bisectriz.
Una bisectriz de un ángulo es una línea, rayo o segmento que divide el ángulo en dos ángulos congruentes, es decir, dos ángulos que tienen la misma medida. En otras palabras, la bisectriz corta el ángulo por la mitad. En el caso de un ángulo de 90 grados, la bisectriz resultante tendría un ángulo de 45 grados a cada lado.
El teorema de la bisectriz en un triángulo
El teorema de la bisectriz establece que, en un triángulo, la bisectriz de un ángulo divide el lado opuesto en segmentos proporcionales a los otros dos lados. Esto puede parecer una afirmación compleja, pero podemos descomponerla y entenderla mejor a través de un ejemplo.
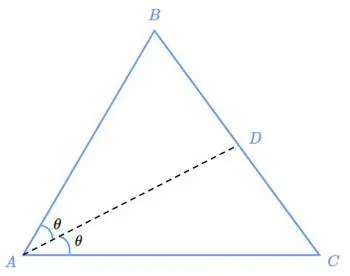
Consideremos un triángulo ABC, donde el ángulo en el vértice A está siendo bisecado por una línea que cruza el lado opuesto BC en el punto D. El teorema nos dice que la proporción entre BD y CD es igual a la proporción entre AB y AC.
Matemáticamente, esto se puede expresar de la siguiente manera:
Este teorema es especialmente útil en la resolución de problemas de geometría que involucran ángulos y segmentos. Puede ayudarnos a encontrar longitudes desconocidas o demostrar propiedades de triángulos y otras figuras geométricas.
Demostración del teorema de la bisectriz
La demostración del teorema de la bisectriz implica el uso de propiedades de triángulos semejantes y la aplicación del teorema de Tales. Aquí hay una explicación breve de cómo se demuestra:
-
Comenzamos con el triángulo ABC y su bisectriz que cruza el lado BC en el punto D.
-
Aplicamos el Teorema de Tales, que establece que si tenemos dos líneas paralelas cortadas por líneas transversales, se crean segmentos proporcionales. En este caso, trazamos una línea paralela a los lados AC y BD que pase por el punto C.
-
Esto nos da dos triángulos semejantes: ACD y ABC, donde los ángulos son iguales y las líneas son paralelas, lo que implica segmentos proporcionales.
-
Usando la propiedad de semejanza de triángulos, podemos afirmar que:
Esta es la igualdad que queríamos demostrar, y así se completa la demostración del teorema.
Ejemplos de aplicaciones del teorema
El teorema de la bisectriz tiene varias aplicaciones en geometría y matemáticas. Algunos de los ejemplos de las aplicaciones más comunes incluyen:
- Resolución de problemas de geometría: El teorema se utiliza para encontrar longitudes desconocidas o ángulos en triángulos y otras figuras geométricas cuando se conocen ciertas relaciones de proporción.
- Demostración de propiedades de triángulos: Se utiliza para demostrar que ciertos triángulos son semejantes o que ciertos puntos están en una línea recta.
- Construcción geométrica: Ayuda en la construcción de ángulos biseccionados con precisión, lo que es útil en diversas aplicaciones de diseño y arquitectura.
- Estudios de trigonometría: El teorema también se aplica en trigonometría para resolver problemas relacionados con senos, cosenos y tangentes.
- Resolución de problemas físicos: Se utiliza en física para comprender las trayectorias de partículas y la dirección de las fuerzas en sistemas físicos.
