Una figura destacada en geometría es el pentágono. Es habitual que por motivos diversos necesitemos hallar el área del pentágono.
Obtener el área y el perímetro de un pentágono es sencillo pero debemos conocer algunas características básicas tales como cuántos lados tiene un pentágono (cinco), qué es un lado o un apotema.
¿Qué es un pentágono?
Un pentágono es un polígono compuesto por cinco lados y cinco vértices.
A su vez, un polígono es una figura geométrica de dos dimensiones con un número finito de segmentos de recta consecutivos no colineales conectados por sus dos extremos, es decir, formando un espacio cerrado.
Los pentágonos son la base de algunos cuerpos geométricos como el prisma pentagonal, o el dodecaedro.
Tipos de pentágonos
Los pentágonos pueden clasificarse en varias categorías, dependiendo de su forma.:
-
Pentágono regular: Es el que tiene todos sus lados y ángulos iguales.
-
Pentágono irregular: No tiene todos sus lados y ángulos iguales.
-
Pentágono convexo: Todos los ángulos internos son menores a 180°.
-
Pentágono cóncavo: Al menos uno de los ángulos interiores es mayor a 180°.
-
Pentágono inscrito: Un pentágono en cuyos vértices todos están sobre una misma circunferencia.
-
Pentágono circunscrito: Es el que tiene su circunferencia tangente a todos sus lados.
Características de un pentágono
A continuación enumeramos las características más significativas de este tipo de figuras geométricas planas:
-
Un pentágono está formado por cinco lados y cinco ángulos. Los diferentes tipos de pentágonos se clasifican en función de sus lados y ángulos.
-
Todos los cinco ángulos internos suman 540º.
-
Si es regular, todos los ángulos internos miden 108° y, por lo tanto, los exteriores miden 72°.
-
El ángulo central del pentágono regular 360° / 5 = 72º. El ángulo central es el que forman dos rectas que unen los dos extremos de un lado al centro de la figura.
-
Está compuesto por cinco diagonales.
-
De cada vértice se pueden trazar dos diagonales a otro vértice.
-
Cuando el pentágono es regular, las diagonales de cada vértice forman tres ángulos de 36° y dividen el pentágono regular en tres triángulos isósceles.
-
El perímetro de un pentágono regular o irregular es la suma de la longitud de todos sus lados. Si es un polígono regular es la longitud de un lado multiplicado por cinco.
¿Cómo se puede encontrar el área de un pentágono?
Existen varias formas de obtener el área de un pentágono regular dependiendo de los datos que disponemos. Una fórmula del área de esta figura geométrica es:
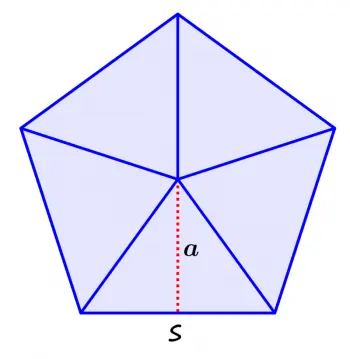
A = (5/2)·c·a
Donde "c" se refiere a la longitud de un lado y "a" se refiere a la longitud del apotema.
Si conocemos el perímetro: la fórmula se convierte en A = p·a/2; donde “p” es el perímetro.
Si conocemos el apotema, podemos utilizar la fórmula:
A = (5 · (a2)) / (4 · tan(36))
Donde "a" se refiere al apotema de la figura.
Calculando el área de un triángulo
El área de un pentágono también se puede calcular dividiéndolo en triángulos:
Si trazamos dos diagonales, de vértice a vértice, sin que se corten se forma tres triàngulos isósceles. La suma del área de estos triángulos es igual al área del pentágono.
Si unimos cada vértice al centro de la figura geométrica nos quedarán 5 triángulos equiláteros. Con la suma de la superficie de estos cinco triángulos también obtendremos la superficie total.