El triángulo, una figura geométrica compuesta por tres segmentos que conectan tres vértices distintos no alineados, representa una de las formas poligonales fundamentales en la geometría. Su relevancia en la ciencia y la tecnología se remonta a tiempos antiguos, dado que es una de las figuras geométricas más esenciales y ampliamente empleadas.
Un rasgo significativo de los triángulos es su invariabilidad, lo que los convierte en elementos cruciales en el diseño arquitectónico, como la Torre Eiffel, basada en una composición de formas triangulares, y la ingeniería, incluyendo estructuras fijas para paneles solares. Además, desempeñan un papel fundamental en la geometría, ya que todos los polígonos pueden descomponerse en triángulos.
Características de los triángulos
Los triángulos son figuras geométricas fundamentales con diversas características que definen su estructura y propiedades. Aquí están algunas de las características más importantes de los triángulos:
- Tres lados: Los triángulos son polígonos que tienen exactamente tres lados. Estos lados son segmentos de línea que conectan tres puntos llamados vértices.
- Tres ángulos: Cada triángulo consta de tres ángulos interiores en sus vértices.
- Suma de ángulos: En un triángulo, la suma de los ángulos internos es igual a 180 grados. Esto es válido para cualquier tipo de triángulo, ya sea equilátero, isósceles o escaleno.
- Lados y ángulos correspondientes: En un triángulo, los lados y ángulos correspondientes son iguales en triángulos congruentes. La congruencia se refiere a la igualdad de forma y tamaño.
- Altura y mediana: En un triángulo, la altura es un segmento de línea perpendicular a un lado y que pasa por el vértice opuesto. La mediana es un segmento que conecta un vértice con el punto medio del lado opuesto.
Tipos de triángulos
Estas figuras geométricas se pueden clasificar siguiendo diferentes criterios:
Por el tamaño de los ángulos interiores puede ser:
- Triángulo acutángulo: todos los ángulos interiores son agudos (menores de 90 grados).
- Triángulo obtusángulo: existe un ángulo mayor de 90 grados.
- Triángulo rectángulo: uno de los ángulos es de 90 grados, un ángulo recto. En este caso, los dos lados que forman un ángulo recto se llaman catetos y el lado opuesto al ángulo recto se llama hipotenusa .
Como en geometría euclidiana la suma de los ángulos de un triángulo es 180º. Por lo tanto, al menos dos ángulos en el triángulo deben ser agudos (menos de 90º)
Por el número de lados iguales estas figuras pueden ser:
- Triángulo escaleno: los tres lados no son iguales.
- Triángulo isósceles: dos lados son iguales. Estos lados se llaman lado , el tercer lado se llama base . En un triángulo isósceles, los ángulos en la base son iguales.
- Triángulo equilátero: los tres lados son iguales. En un triángulo equilátero, todos los ángulos son iguales a 60°.
Calcular el área y el perímetro de un triángulo
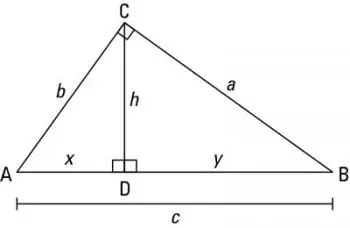
Basándonos en la figura de la parte inferior, para obtener el perímetro y área de un triángulo, podemos utilizar las siguientes fórmulas:
Perímetro
Para calcular el perímetro simplemente tenemos que sumar la longitud de los lados de la figura: a + b + c.
Area
La fórmula para sacar el área de un triángulo es la mitad del producto de la base (no de los lados) por la altura:
A = (b · h) / 2
En el caso que desconozcamos la altura podemos aplicar la fórmula de Herón.
Donde:
-
a, b y c corresponde a los tres lados de la figura geométrica.
-
A es el área
-
s es el semiperímetro (se halla el perímetro y se divide por dos):
En el caso de un triángulo rectángulo, uno de los catetos es la base y el otro corresponde a la altura la altura. De esta forma resulta más sencillo calcular el área.
Propiedades y teoremas
Teorema de Pitágoras
El teorema de Pitágoras es uno de los resultados geométricos más famosos y útiles. Se aplica a triángulos rectángulos, aquellos con un ángulo recto (90 grados). El teorema establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los otros dos lados. Matemáticamente, se expresa como:
a² + b² = c²
Donde "a" y "b" son las longitudes de los catetos y "c" es la longitud de la hipotenusa.
El teorema de Pitágoras es fundamental en geometría y trigonometría y se aplica en una amplia variedad de problemas, desde cálculos de distancias en mapas hasta la resolución de ecuaciones cuadráticas.
Teorema de la Bisectriz
El teorema de la Bisectriz se refiere a la bisectriz de un ángulo en un triángulo. Establece que la bisectriz de un ángulo divide el lado opuesto al ángulo en dos segmentos que son proporcionales a los otros dos lados del triángulo. Matemáticamente, se expresa como:
a / d = b / e
Donde "a" y "b" son las longitudes de los lados del triángulo, y "d" y "e" son las longitudes de los segmentos en los que la bisectriz divide el lado opuesto.
Este teorema es útil para calcular segmentos en triángulos y encontrar puntos de intersección en ángulos bisectores.
Teorema de Tales
El teorema de Tales es una herramienta poderosa para relacionar segmentos en triángulos semejantes. Establece que si una línea paralela corta dos lados de un triángulo, divide estos lados en segmentos proporcionales. Matemáticamente, se expresa como:
m / n = p / q
Donde "m" y "n" son las longitudes de los segmentos en un lado del triángulo, y "p" y "q" son las longitudes de los segmentos correspondientes en el otro lado.
El teorema de Tales es fundamental en la resolución de problemas geométricos y en la demostración de propiedades de triángulos semejantes.
