El teorema de Gauss para el campo eléctrico establece que el flujo de un campo eléctrico a través de una superficie cerrada (superfície gaussiana) está dado por el cociente entre la carga eléctrica total dentro de la superficie dividido entre la constante dieléctrica absoluta del medio (ε0). Cualquier carga puntual externa a la superficie no contribuye de ninguna manera al flujo total.
La ecuación de Gauss forma parte de las cuatro ecuaciones de Maxwell.
El campo eléctrico producido por dos objetos cargados estáticos puede obtenerse por dos procedimientos equivalentes: aplicando la ley de Coulomb o mediante la ley de Gauss. La ley de Coulomb es una forma más simpre y directa de expresar la fuerza eléctrica. Por otro lado, la ley de Gauss es más sutil, más elegante y, a veces, más útil.
El teorema de Gauss tiene una utilidad muy práctica. En su formulación física relativa a los campos eléctricos se traduce en última instancia en una fórmula simple, utilizable por todos y con implicaciones prácticas muy significativas.
El flujo de cargas que atraviesan la superfície gausiana es proporcional al número de lineas de campo que la cruzan.
Enunciado del teorema de Gauss
Aquí está el enunciado del teorema de Gauss para el campo eléctrico : el flujo de un campo eléctrico a través de una superficie cerrada está dado por la relación entre la carga eléctrica total dentro de la superficie y la constante dieléctrica absoluta del medio .
Fórmula de la ley de Gauss
En cuanto a la fórmula del teorema de Gauss para el campo eléctrico, podemos escribir
La declaración de Gauss proporciona una forma rápida y sencilla de calcular el flujo del campo eléctrico a través de una superficie cerrada. Simplemente se calcula la suma algebraica de todas las cargas que están dentro de la superficie y se divide por la constante dieléctrica absoluta.
Es importante destacar algunos aspectos:
-
Si pensamos en el vacío podemos sustituir la constante dieléctrica absoluta del medio εm por la constante dieléctrica del vacío cuyo valor conocemos.
-
Para calcular la suma algebraica de todas las cargas internas, es necesario tener en cuenta los signos de las cargas , que pueden ser cargas positivas o negativas.
-
La superficie puede tener cualquier forma siempre que esté cerrada.
-
Lo que importa es la carga total dentro del área de la superfície. Si hubiera otras cargas ubicadas fuera de la superficie, no deben considerarse a los efectos del cálculo del caudal.
-
El teorema es válido para cualquier tipo de campo eléctrico, no necesariamente uniforme en el espacio. La fórmula también es válida para cualquier configuración de carga.
Ejemplo de la ley de Gauss
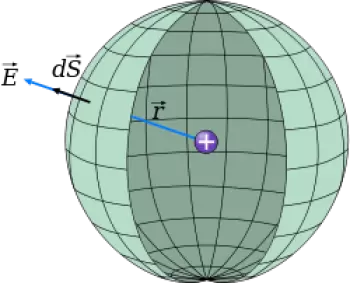
Supongamos que queremos calcular el campo eléctrico producido por una carga puntual y, usemos la ley de Gauss para encontrarla.
En nuestro ejemplo imaginemos una superficie gaussiana esferica de radio r con una carga (q) contenida en su centro. Para calcular la integral de flujo supondremos que, por la simetría del problema, E debe tener la dirección radial hacia fuera de la carga (q). Esto implica que E es paralelo a dS en cada punto de la superfície de la espera.
También por la simetría debemos suponer que E depende únicamente de la distancia r desde la carga q al punto consideado, de forma que E tendrá el mismo valor para cualquier punto sobre la esfera, y será constante en la integración.
En estas condiciones, el cálculco del flujo a través de la superfície esférica será:
Φ=E(4·π·r²)
Ya que la integral es simplemente el área de la superficie de la esfera. Como la carga total contenida dentro de nuestra esfera es q, la ley de Gauss nos da: