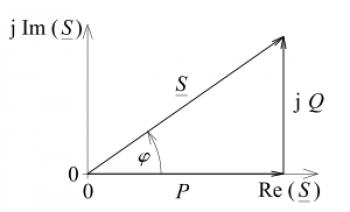
El triángulo de potencias, también conocido como triángulo de Watt, es una representación gráfica utilizada en la teoría de la electricidad para analizar la distribución de potencia en un circuito de corriente alterna (CA).
Se basa en las propiedades trigonométricas de un triángulo rectángulo, lo que permite calcular y comprender la relación entre las tres potencias fundamentales de un sistema eléctrico:
- Potencia aparente (\( S \)): Representa la potencia total suministrada al circuito y se mide en voltiamperios (VA). Es la combinación vectorial de la potencia activa y la reactiva.
- Potencia activa (\( P \)): Es la potencia útil que se transforma en trabajo real, como la iluminación o el movimiento de motores. Se mide en vatios (W).
- Potencia reactiva (\( Q \)): Es la potencia que no realiza trabajo útil pero es necesaria para el funcionamiento de equipos con elementos inductivos (como transformadores y motores). Se mide en voltiamperios reactivos (VAR).
Fórmula del triángulo de potencias
El triángulo está compuesto por tres lados, donde:
- La hipotenusa representa la potencia aparente (\( S \)).
- El cateto adyacente es la potencia activa (\( P \)), relacionada con el coseno del ángulo de fase (\( \cos\theta \)).
- El cateto opuesto es la potencia reactiva (\( Q \)), relacionada con el seno del ángulo de fase (\(\sin\theta \)).
- Matemáticamente, la relación entre estas potencias se expresa mediante el teorema de Pitágoras:
\[ S^2 = P^2 + Q^2 \]
El factor de potencia (FP) se define como la relación entre la potencia activa y la potencia aparente:
\[ FP = \cos\theta = \frac{P}{S} \]
Cuando el factor de potencia es bajo, significa que hay una alta proporción de potencia reactiva, lo que reduce la eficiencia del sistema eléctrico.
Ejemplos prácticos del triángulo de potencias
A continuació móstramos tres ejemplos prácticos
Motor eléctrico con factor de potencia bajo
Un motor de inducción consume 10 kW de potencia activa y tiene una potencia reactiva de 6 kVAR debido a su naturaleza inductiva.
La potencia aparente será:
\[ S = \sqrt{(10^2 + 6^2)} = \sqrt{100 + 36} = \sqrt{136} \approx 11.66 \text{ kVA} \]
Sistema de iluminación con corrección de factor de potencia
Un conjunto de lámparas LED consume 5 kW con una potencia reactiva de 1 kVAR.
La potencia aparente será:
\[ S = \sqrt{(5^2 + 1^2)} = \sqrt{25 + 1} = \sqrt{26} \approx 5.1 \text{ kVA} \]
Transformador con carga inductiva
Un transformador suministra 50 kW a un sistema con una carga inductiva que requiere 30 kVAR.
La potencia aparente del sistema será:
\[ S = \sqrt{(50^2 + 30^2)} = \sqrt{2500 + 900} = \sqrt{3400} \approx 58.3 \text{ kVA} \]
¿Para qué sirve el triángulo de potencias?
El triángulo de potencias es una herramienta fundamental en el análisis y diseño de sistemas eléctricos. Sus aplicaciones incluyen:
Cálculo de la potencia eléctrica
Permite determinar la distribución de potencia en un circuito:
- La potencia aparente (S) total suministrada.
- La potencia activa (P), que se convierte en energía útil.
- La potencia reactiva (Q), que representa la energía intercambiada entre componentes inductivos y capacitivos.
Optimización del rendimiento del circuito
Al conocer la distribución de potencias, se pueden minimizar las pérdidas energéticas y mejorar el factor de potencia, lo que reduce el consumo innecesario de energía reactiva y optimiza el uso de la red eléctrica.
Diseño de sistemas eléctricos
Se usa para el dimensionamiento de equipos eléctricos, asegurando que los transformadores, generadores y cables sean adecuados para manejar la potencia requerida sin sobrecarga ni pérdidas excesivas.
Corrección del factor de potencia
Muchos sistemas eléctricos industriales requieren bancos de condensadores para compensar la potencia reactiva y mejorar el factor de potencia, reduciendo así la demanda de energía de la red y disminuyendo costos operativos.
Análisis de fallas y mantenimiento preventivo
El triángulo de potencias permite detectar problemas en sistemas eléctricos, como pérdidas de energía debidas a alta reactancia o desajustes en la carga, ayudando a prevenir fallas y optimizar el mantenimiento.
Ejercicio resuelto sobre el triángulo de potencias
Enunciado:
Se tiene un circuito eléctrico con una potencia aparente de 800 VA y un factor de potencia de 0,8. Calcular la potencia activa y la potencia reactiva del circuito.
Solución:
Primero, podemos calcular la potencia activa (P) del circuito utilizando la fórmula P = S x cos(θ), donde θ es el ángulo de fase entre la corriente y el voltaje. En este caso, como el factor de potencia (FP) es igual a 0,8, sabemos que cos(θ) = FP = 0,8. Por lo tanto, podemos calcular la potencia activa como sigue:
\[
P = 800 \, VA \times 0.8 = 640 \, W
\]
La potencia activa del circuito es de 640 vatios.
Luego, podemos calcular la potencia reactiva (Q) del circuito utilizando la fórmula Q = S x sen(θ). Sabemos que el ángulo de fase (θ) se puede calcular a partir del factor de potencia utilizando la siguiente fórmula:
\[
\cos(\theta) = \text{FP} \quad \Rightarrow \quad \sin(\theta) = \sqrt{1 - \cos^2(\theta)}
\]
En este caso, como FP = 0,8, podemos calcular sen(θ) como sigue:
\[
\sin(\theta) = \sqrt{1 - 0.8^2} = \sqrt{1 - 0.64} = \sqrt{0.36} = 0.6
\]
Por lo tanto, podemos calcular la potencia reactiva como sigue:
\[
Q = 800 \, VA \times 0.6 = 480 \, VAR
\]
La potencia reactiva del circuito es de 480 voltiamperios reactivos.
Por lo tanto, la potencia activa del circuito es de 640 W y la potencia reactiva es de 480 VAR.